マトリックス法計算例

1.架構図

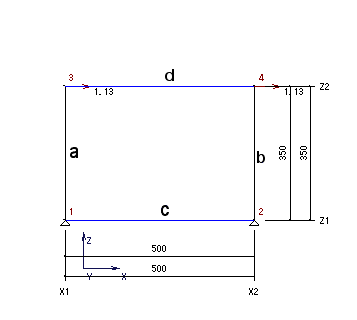
2.断面

節点	b × d (cm)	L (cm)	I (cm^4)	A (cm^2)	As (cm^2)	G (t/cm^2)	E (t/cm^2)
1-2 a	50.0 × 50.0	350	520833	2500	1666.67	900	210
2-4 d	25.0 × 50.0	500	260417	1250	833.33	900	210
3-4 b	50.0 × 50.0	350	520833	2500	1666.67	900	210
1-3 c	25.0 × 50.0	500	260417	1250	833.33	900	210

符号
I：断面二次モーメント
A：断面積
As：せん断用断面積
G：せん断弾性係数
E：ヤング係数

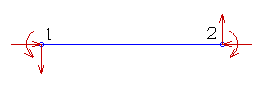
3.部材端荷重と部材応力の符号

正方向荷重	正方向の応力
負方向の荷重	負方向の応力

4.一般的な部材剛性マトリックス

K11	=		EA/L	0	0
			0	1/(1+2γ)*12EI/L^3	1/(1+2γ)*6EI/L^2
			0	1/(1+2γ)*6EI/L^2	(1-γ/2)/(1+2γ)*4EI/L

K12	=		-EA/L	0	0
			0	-1/(1+2γ)*12EI/L^3	1/(1+2γ)*6EI/L^2
			0	-1/(1+2γ)*6EI/L^2	(1-γ)/(1+γ)*2EI/L

K21	=		-EA/L	0	0
			0	-1/(1+2γ)*12EI/L^3	-1/(1+2γ)*6EI/L^2
			0	1/(1+2γ)*6EI/L^2	(1-γ)/(1+γ)*2EI/L

K22	=		EA/L	0	0
			0	1/(1+2γ)*12EI/L^3	-1/(1+2γ)*6EI/L^2
			0	-1/(1+2γ)*6EI/L^2	(1-γ/2)/(1+2γ)*2EI/L

*γ = 6EI/GAsL^2

5.座標変換マトリックス
水平部材
α = 0 (rad)

Th	=		cosα	-sinα	0		=		1	0	0
			sinα	cosα	0				0	1	0
			0	0	1				0	0	1

鉛直部材
α = π/2 (rad)

Th	=		cosα	-sinα	0		=		0	-1	0
			sinα	cosα	0				1	0	0
			0	0	1				0	0	1

6.部材剛性マトリックス
水平部材
部材c = 部材d
γ = 0.00175
K11' = Th × K11 × Tht

K11'	=		EA/L	0	0
			0	1/(1+2γ)*12EI/L^3	1/(1+2γ)*6EI/L^2
			0	1/(1+2γ)*6EI/L^2	(1+γ/2)/(1+2γ)*4EI/L

	=		525	0	0
			0	5.231689088	1307.922272
			0	1307.922272	436355.568

K12' = Th × K12 × Tht

K12'	=		-EA/L	0	0
			0	-1/(1+2γ)*12EI/L^3	1/(1+2γ)*6EI/L^2
			0	-1/(1+2γ)*6EI/L^2	(1-γ)/(1+γ)*2EI/L

	=		-525	0	0
			0	-5.231689088	1307.922272
			0	-1307.922272	217985.7125

K21' = Th × K21 × Tht

K21'	=		-EA/L	0	0
			0	-1/(1+2γ)*12EI/L^3	-1/(1+2γ)*6EI/L^2
			0	1/(1+2γ)*6EI/L^2	(1-γ)/(1+γ)*2EI/L

	=		-525	0	0
			0	-5.231689088	-1307.922272
			0	1307.922272	217985.7125

K22' = Th × K22 × Tht

K22'	=		EA/L	0	0
			0	1/(1+2γ)*12EI/L^3	-1/(1+2γ)*6EI/L^2
			0	-1/(1+2γ)*6EI/L^2	(1-γ/2)/(1+2γ)*2EI/L

	=		525	0	0
			0	5.231689088	-1307.922272
			0	-1307.922272	436355.568

鉛直部材
部材a = 部材c
γ = 0.003571429
K11' = Th × K11 × Tht

K11'	=		1/(1+2γ)*12EI/L^3	0	-1/(1+2γ)*6EI/L^2
			0	EA/L	0
			-1/(1+2γ)*6EI/L^2	0	(1+γ/2)/(1+2γ)*4EI/L

	=		30.39513678	0	-5319.148936
			0	1500	0
			-5319.14836	0	1243351.064

K12' = Th × K12 × Tht

K12'	=		-1/(1+2γ)*12EI/L^3	0	-1/(1+2γ)*6EI/L^2
			0	-EA/L	0
			1/(1+2γ)*6EI/L^2	0	(1-γ)/(1+γ)*2EI/L

	=		-30.39513678	0	-5319.148936
			0	-1500	0
			5319.14836	0	620551.6014

K21' = Th × K21 × Tht

K21'	=		-1/(1+2γ)*12EI/L^3	0	1/(1+2γ)*6EI/L^2
			0	-EA/L	0
			-1/(1+2γ)*6EI/L^2	0	(1+γ/2)/(1+2γ)*4EI/L

	=		-30.39513678	0	5319.148936
			0	-1500	0
			-5319.14836	0	620551.6014

K22' = Th × K22 × Tht

K22'	=		1/(1+2γ)*12EI/L^3	0	1/(1+2γ)*6EI/L^2
			0	EA/L	0
			1/(1+2γ)*6EI/L^2	0	(1-γ)/(1+γ)*2EI/L

	=		30.39513678	0	5319.148936
			0	1500	0
			5319.14836	0	1243351.064

7.全体マトリックス
{P} = K{δ}

P1

=

(K11')a+(K11')c

(K12')a

0

(K12')c

×

d1

P2

(K21')a

(K22')a+(K11')d

(K12')d

0

d2

P3

0

(K21')d

(K22')d+(K22')b

(K21')b

d3

P4

(K21')c

0

(K12')b

(K11')b+(K22')c

d4

	Px1		=		5.554E+02	0	-5.139E+03	-3.040E+01	0	-5.319E+03	0	0	0	-5.250E+02	0	0		×		dx1
	Py1				0	1.505E+03	1.308E+03	0	-1.500E+03	0	0	0	0	0	-5.232E+00	1.308E+03				dy1
	M1				-5.319E+03	1.308E+03	1.680E+03	5.319E+03	0	6.206E+05	0	0	0	0	-1.308E+03	2.180E+05				r1
	Px2				-3.040E+01	0	5.319E+03	5.554E+02	0	3.319E+03	-5.250E+02	0	0	0	0	0				dx2
	Py2				0	-1.500E+03	0	0	1.505E+03	1.308E+03	0	-5.232E+00	1.308E+03	0	0	0				dy2
	M2				-5.319E+03	0	6.206E+05	5.319E+03	1.308E+03	1.680E+06	0	-1.308E+03	2.180E+05	0	0	0				r1
	Px3				0	0	0	-5.250E+02	0	0	5.551E+02	0	5.319E+03	-3.061E+01	0	5.319E+03				dx3
	Py3				0	0	0	0	-5.232E+00	-1.308E+03	0	1.505E+03	-1.308E+03	0	-1.500E+03	0				dy3
	M3				0	0	0	0	1.308E+03	2.180E+05	5.319E+03	-1.308E+03	1.680E+06	-5.357E+03	0	6.206E+05				r3
	Px4				-5.250E+02	0	0	0	0	0	-3.040E+01	0	-5.319E+03	5.554E+02	0	-5.319E+03				dx4
	Py4				0	-5.232E+00	-1.308E+03	0	0	0	0	-1.500E+03	0	0	1.505E+03	-1.308E+03				dy4
	M4				0	1.308E+03	2.180E+05	0	0	0	5.319E+03	0	6.206E+05	-5.319E+03	-1.308E+03	1.680E+06				dx4

8.適合条件
dx1 = 0
dy1 = 0
dx4 = 0
dy4 = 0
Px2 = 1.13(t)
Px3 = 1.13(t)

9.変位量の計算
{δ} = K^(-1){P}

r1

=

90972E-07

-1.347E-04

-3.221E-07

1.196E-08

-1.323E-04

3.221E-07

3.601E-07

1.565E-07

=

0

dx2

-1.347E-04

6.373E-02

2.320E-04

-1.352E-04

6.278E-02

-2.320E-04

-1.328E-04

-1.323E-04

1.130E+00

dy2

-3.221E-07

2.320E-04

6.661E-04

-1.004E-06

2.320E-04

5.709E-07

-1.004E-06

-3.221E-07

0

r2

1.196E-08

-1.352E-04

-1.004E-06

9.999E-07

-1.328E-04

1.004E-06

1.592E-07

3.601E-07

0

dx3

-1.323E-04

6.278E-02

2.320E-04

-1.328E-04

6.373E-02

-2.320E-04

-1.352E-04

-1.347E-04

1.130E+00

dy3

3.221E-07

-2.320E-04

5.709E-07

1.004E-06

-2.320E-04

6.661E-04

1.004E-06

3.221E-07

0

r3

3.601E-07

-1.328E-04

-1.004E-06

1.592E-07

-1.352E-04

1.004E-06

9.999E-07

1.196E-08

0

r4

1.565E-07

-1.323E-04

-3.221E-07

3.601E-07

-1.347E-04

3.221E-07

1.196E-08

9.972E-07

0

	=		-3.017E-04
			1.430E-01
			5.244E-04
			-3.028E-04
			1.430E-01
			-5.244E-04
			-3.028E-04
			-3.017E-04

10.各部材の応力の計算
・水平部材
c部材 Pc1 = (K11')c × d1 + (K12')c × d4

Px1c

=

5.250E+02

0

0

×

0

+

-5.250E+02

0

0

×

0

Py1c

0

5.232E+00

1.308E+03

0

0

-5.232E+00

1.308E+03

0

m1c

0

1.308E+03

4.364E+05

-3.017E-04

0

-1.308E+03

2.180E+05

-3.017E-04

	=		0		t
			-7.892E-01		t
			-1.974E+02		t・cm

d部材 Pd1 = (K11')d × d2 + (K12')d × d3

Px1d

=

5.250E+02

0

0

×

1.430E-01

+

-5.250E+02

0

0

×

1.430E-01

Py1d

0

5.232E+00

1.308E+03

5.244E-04

0

-5.232E+00

1.308E+03

-5.244E-04

m1d

0

1.308E+03

4.364E+05

-3.028E-04

0

-1.308E+03

2.180E+05

-3.028E-04

	=		0		t
			-7.865E-01		t
			-1.968E+02		t・cm

鉛直部材
ｂ部材
Pb1' = (K11')b × d4 + (K12')b × d3

Px1b'

=

3.040E+01

0

-5.319E+03

×

0

+

-3.040E+01

0

-5.319E+03

×

1.430E-01

Py1b'

0

1.500E+03

0

0

0

-1.500E+03

0

-5.244E-04

m1b'

-5.319E+03

0

1.243E+06

-3.017E-04

5.319E+03

0

6.206E+05

-3.028E-04

	=		-1.130E+00		t
			7.865E-01		t
			1.974E+02		t・cm

Pb1'を部材座標系に変換
Pb1 = Tt × Pb1'

	Px1b		=		0	1	0		×		-1.130E+00		t
	Py1b				-1	0	0				7.865E-01		t
	m1b				0	0	1				1.974E+02		t・cm

	=		7.865E-01		t
			1.130E+00		t
			1.974E+02		t・cm

Pb2' = (K22')b × d3 + (K21')b × d4

Px2b'

=

3.040E+01

0

5.319E+03

×

1.430E-01

+

-3.061E+01

0

5.319E+03

×

0

Py2b'

0

1.500E+03

0

-5.244E-04

0

-1.500E+03

0

0

m2b'

5.319E+03

0

1.243E+06

-3.028E-04

-5.357E+03

0

6.206E+05

-3.017E-04

	=		1.130E+00		t
			-7.865E-01		t
			1.974E+02		t・cm

Pb2'を部材座標系に変換
Pb2 = Tt × Pb2'

	Px2b		=		0	1	0		×		1.130E+00		t
	Py2b				-1	0	0				-7.865E-01		t
	m2b				0	0	1				1.968E+02		t・cm

	=		-7.865E-01		t
			-1.130E+00		t
			1.968E+02		t・cm

Pa1' = (K11')a × d1 + (K12')a × d2

Px1a'

=

3.040E+01

0

-5.319E+03

×

0

+

-3.040E+01

0

-5.319E+03

×

1.430E-01

Py1a'

0

1.500E+03

0

0

0

-1.500E+03

0

-5.244E-04

m1a'

-5.319E+03

0

1.243E+06

-3.017E-04

5.319E+03

0

6.206E+05

-3.028E-04

	=		3.210E+00		t
			0		t
			-7.503E+02		t・cm

Pa1'を部材座標系に変換
Pa1 = Tt × Pa1'

	Px1a		=		0	1	0		×		3.210E+00		t
	Py1a				-1	0	0				0		t
	m1a				0	0	1				-7.503E+02		t・cm

	=		0		t
			-3.210E+00		t
			-7.503E+02		t・cm

Pa2' = (K22')a × d2 + (K21')a × d1

Px2a'

=

3.040E+01

0

5.319E+03

×

1.430E-01

+

-3.061E+01

0

5.319E+03

×

0

Py2a'

0

1.500E+03

0

5.244E-04

0

-1.500E+03

0

0

m2a'

5.319E+03

0

1.243E+06

-3.028E-04

-5.357E+03

0

6.206E+05

-3.017E-04

	=		1.130E+00		t
			7.865E-01		t
			1.974E+02		t・cm

Pa2'を部材座標系に変換
Pa2 = Tt × Pa2'

	Px2a		=		0	1	0		×		1.130E+00		t
	Py2a				-1	0	0				7.865E-01		t
	m2a				0	0	1				1.968E+02		t・cm

	=		7.865E-01		t
			-1.130E+00		t
			1.968E+02		t・cm

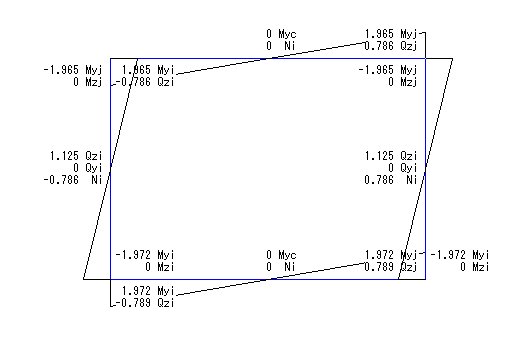
FAP-3による応力計算結果